RD Sharma Solutions for Class 8 Chapter 15 Understanding Shapes- I (Polygons)

RD Sharma Solutions for Class 8 Chapter 15 Understanding Shapes- I (Polygons) Free Online

EXERCISE 15.1 PAGE NO: 15.5

1. Draw rough diagrams to illustrate the following:
(i) Open curve
(ii) Closed curve

Solution:

Here is the illustration of

(i) Open curve

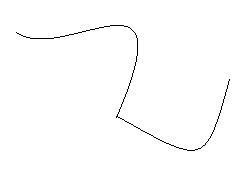
(ii) Closed curve

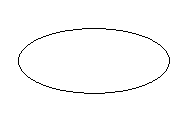
2. Classify the following curves as open or closed:

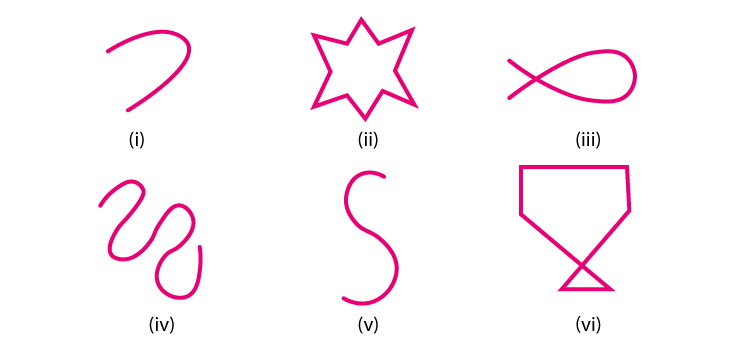
Solution:

(i) Open curve

(ii) Closed curve

(iii) Closed curve

(iv) Open curve

(v) Open curve

(vi) Closed curve

3. Draw a polygon and shade its interior. Also draw its diagonals, if any.

Solution:

Here is the polygon with diagonals and with its interior shaded.

4. Illustrate, if possible each one of the following with a rough diagram.
(i) A closed curve that is not a polygon.
(ii) An open curve made up entirely of line segments.
(iii) A polygon with two sides.

Solution:

(i) A closed curve that is not a polygon.

(ii) An open curve made up entirely of line segments.

(iii) A polygon with two sides.

A polygon with two sides is not possible because, a polygon should have minimum three sides.

5. Following are some figures: Classify each of these figures on the basis of the following:

(i) Simple curve (ii) Simple closed curve (iii) Polygon

(iv) Convex polygon (v) Concave polygon (vi) Not a curve

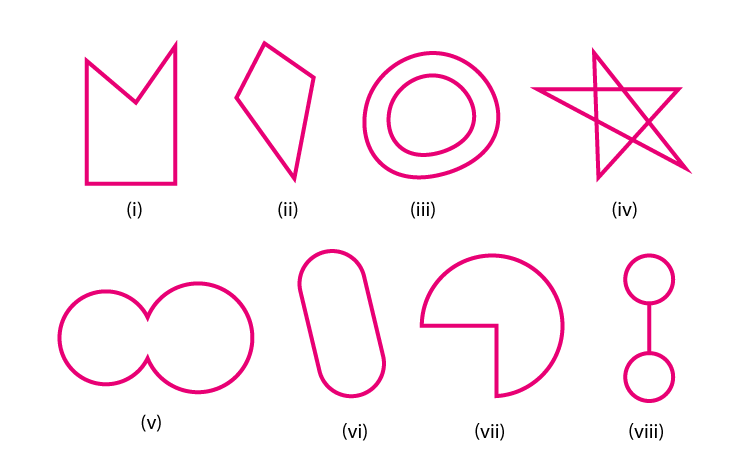
Solution:

(i) It is a Simple Closed curve and a concave polygon. This is a simple closed curve and as a concave polygon all the vertices are not pointing outwards.

(ii) It is a Simple closed curve and a convex polygon. This is a simple closed curve and as a convex polygon all the vertices are pointing outwards.

(iii) It is Not a curve and hence it is not a polygon.

(iv) It is Not a curve and hence it is not a polygon.

(v) It is a Simple closed curve but not a polygon.

(vi) It is a Simple closed curve but not a polygon.

(vii) It is a Simple closed curve but not a polygon.

(viii) It is a Simple closed curve but not a polygon.

6. How many diagonals does each of the following have?
(i) A convex quadrilateral
(ii) A regular hexagon
(iii) A triangle

Solution:

(i) A convex quadrilateral

For a convex quadrilateral we shall use the formula n(n-3)/2

So, number of diagonals = 4(4-3)/2 = 4/2 = 2

A convex quadrilateral has 2 diagonals.

(ii) A regular hexagon

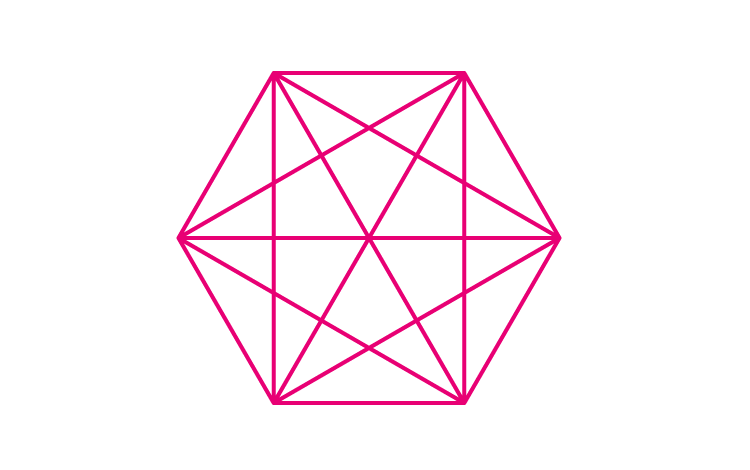
For a regular hexagon we shall use the formula n(n-3)/2

So, number of diagonals = 6(6-3)/2 = 18/2 = 9

A regular hexagon has 9 diagonals.

(iii) A triangle

For a triangle we shall use the formula n(n-3)/2

So, number of diagonals = 3(3-3)/2 = 0/2 = 0

A triangle has no diagonals.

7. What is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides

Solution:

Regular Polygon: A regular polygon is an enclosed figure. In a regular polygon minimum sides are three.

(i) 3 sides

A regular polygon with 3 sides is known as Equilateral triangle.

(ii) 4 sides

A regular polygon with 4 sides is known as Rhombus.

(iii) 6 sides

A regular polygon with 6 sides is known as Regular hexagon.