RD Sharma Solutions for Class 6 Chapter 6 Fractions Free Online
Exercise 6.1 PAGE: 6.4
1. Write the fraction representing the shaded portion:

Solution:
We know that
Fraction of the shaded portion = Number of shaded parts/ Total number of parts
(i) From the figure we know that
Total number of parts = 3
Number of parts which are shaded = 2
So we get
Fraction of the shaded portion = 2/3
(ii) From the figure we know that
Total number of parts = 15
Number of parts which are shaded = 11
So we get
Fraction of the shaded portion = 11/15
(iii) From the figure we know that
Total number of parts = 9
Number of parts which are shaded = 8
So we get
Fraction of the shaded portion = 8/9
(iv) From the figure we know that
Total number of parts = 7
Number of parts which are shaded = 3
So we get
Fraction of the shaded portion = 3/7
(v) From the figure we know that
Total number of parts = 9
Number of parts which are shaded = 4
So we get
Fraction of the shaded portion = 4/9
(vi) From the figure we know that
Total number of parts = 4
Number of parts which are shaded = 2
So we get
Fraction of the shaded portion = 2/4 = 1/2
(vii) From the figure we know that
Total number of parts = 2
Number of parts which are shaded = 1
So we get
Fraction of the shaded portion = 1/2
(viii) From the figure we know that
Total number of parts = 5
Number of parts which are shaded = 1
So we get
Fraction of the shaded portion = 1/5
(ix) From the figure we know that
Total number of parts = 4
Number of parts which are shaded = 1
So we get
Fraction of the shaded portion = 1/4
2. Write the fraction representing the shaded parts:

Solution:
We know that
Fraction of the shaded portion = Number of shaded parts/ Total number of parts
(i) From the figure we know that
Total number of parts = 9
Number of parts which are shaded = 3
So we get
Fraction of the shaded portion = 3/9 = 1/3
(ii) From the figure we know that
Total number of parts = 8
Number of parts which are shaded = 4
So we get
Fraction of the shaded portion = 4/8 = 1/2
(iii) From the figure we know that
Total number of parts = 12
Number of parts which are shaded = 3
So we get
Fraction of the shaded portion = 3/12 = 1/4
(iv) From the figure we know that
Total number of parts = 10
Number of parts which are shaded = 5
So we get
Fraction of the shaded portion = 5/10 = 1/2
3. Write the fraction representing the shaded portion:

Solution:
We know that
Fraction of the shaded portion = Number of shaded parts/ Total number of parts
(i) From the figure we know that
Total number of parts = 2
Number of parts which are shaded = 1
So we get
Fraction of the shaded portion = 1/2
(ii) From the figure we know that
Total number of parts = 8
Number of parts which are shaded = 4
So we get
Fraction of the shaded portion = 4/8
4. Colour the part according to the fraction given:

Solution:

5. What fraction of an hour is 20 minutes?
Solution:
We know that
Minutes in an hour = 60
So 20 minutes of an hour = 20/ 60 = 1/3
Therefore, 1/3 of an hour is 20 minutes.
6. Write the natural numbers from 2 to 12. What fraction of them are prime numbers?
Solution:
We know that natural numbers from 2 to 12 are
2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12
The prime numbers from 2 to 12 are
2, 3, 5, 7 and 11
So 5 numbers are prime among the 11 numbers
Therefore, 5/11 of them are prime numbers.
7. Write the natural numbers from 102 to 113. What fraction of them are prime numbers?
Solution:
We know that the natural numbers from 102 to 113 are
102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112 and 113
The prime numbers from 102 to 113 are
103, 107, 109 and 113
So 4 numbers are prime among the 12 numbers
We get the fraction of prime numbers = 4/ 12 = 1/3
Therefore, 1/3 fraction of them are prime numbers.
8. Mukesh has a box of 24 pencils. He gives half of them to Sunita. How many does Sunita get? How many does Mukesh still have?
Solution:
Number of pencils Mukesh has = 24
He gives half of them to Sunita = 24/ 2 = 12
So the number of pencils Mukesh still has = 24 – 12 = 12
Therefore, Mukesh gives 12 pencils to Sunita and still has 12 pencils.
9. Kavita has 44 cassettes. She gives ¾ of them to Sonia. How many does Sonia get? How many does Kavita keep?
Solution:
Number of cassettes Kavita has = 44
She gives ¾ of them to Sonia = ¾ (44) = 33
So the number of cassettes Kavita keeps = 44 – 33 = 11
Therefore, Kavita gives 33 cassettes to Sonia and still keeps 11 cassettes.
10. Shikhas has three frocks that she wears when playing. The material is good, but the colours are faded. Her mother buys some blue dye and uses it on two of the frocks. What fraction of all of the Shikha play frocks did her mother dye?
Solution:
Number of frocks = 3
Number of frocks Shikha’s mother dyed = 2
So the fraction of dyed frocks = 2/3
Hence, Shikha’s mother dyed 2/3 fraction of all of Shika’s play frocks.
Exercise 6.2 page: 6.7
1. Represent 2/5 on a number line.
Solution:
The fraction 2/5 is represented on a number line as given below:

2. Represent 0/10, 1/10, 5/10 and 10/10 on a number line.
Solution:
The fraction 0/10, 1/10, 5/10 and 10/10 are represented on a number line as given below:

3. Represent 2/7, 5/7 and 6/7 on a number line.
Solution:
The fraction 2/7, 5/7 and 6/7 are represented on a number line as given below:

4. How many fractions lie between 0 and 1.
Solution:
Infinite number of fractions lie between 0 and 1
This can be done by taking numerator less than denominator in a fraction.
5. Represent 0/8 and 8/8 on a number line.
Solution:
The fraction 0/8 and 8/8 are represented on a number line as given below:

Exercise 6.3 page: 6.8
1. Write each of the following divisions as fractions:
(i) 6 ÷ 3
(ii) 25 ÷ 5
(iii) 125 ÷ 50
(iv) 55 ÷ 11
Solution:
(i) The division 6 ÷ 3 can be written as 6/3.
(ii) The division 25 ÷ 5 can be written as 25/5.
(iii) The division 125 ÷ 50 can be written as 125/50.
(iv) The division 55 ÷ 11 can be written as 55/11.
2. Write each of the following fractions as divisions:
(i) 9/7
(ii) 3/11
(iii) 90/63
(iv) 1/5
Solution:
(i) The fraction 9/7 can be written as 9 ÷ 7.
(ii) The fraction 3/11 can be written as 3 ÷ 11.
(iii) The fraction 90/63 can be written as 90 ÷ 63.
(iv) The fraction 1/5 can be written as 1 ÷ 5.
Exercise 6.4 page: 6.11
1. Convert each of the following into a mixed fraction:
(i) 28/9
(ii) 226/15
(iii) 145/9
(iv) 128/5
Solution:
(i) 28/9 can be written as a mixed fraction as 3 1/9.
(ii) 226/15 can be written as a mixed fraction as 15 1/15.
(iii) 145/9 can be written as a mixed fraction as 16 1/9.
(iv) 128/5 can be written as a mixed fraction as 25 3/5.
2. Convert each of the following into an improper fraction:
(i) 7 ¼
(ii) 8 5/7
(iii) 5 3/10
(iv) 12 7/15
Solution:
(i) 7 ¼ can be written as an improper fraction as 29/9.
(ii) 8 5/7 can be written as an improper fraction as 61/7.
(iii) 5 3/10 can be written as an improper fraction as 53/10.
(iv) 12 7/15 can be written as an improper fraction as 187/15.
Exercise 6.5 page: 6.15
1. Write the fractions and check whether they are equivalent or not:

Solution:
(i) We know that
Fraction = ½
Fraction = 2/4 = 1/2
Fraction = 3/6 = ½
Fraction = 4/8 = ½
Hence, they are equivalent.
(ii) We know that
Fraction = 5/15 = 1/3
Fraction = 3/9 = 1/3
Fraction = 2/6 = 1/3
Fraction = 1/3
Hence, they are equivalent.
2. Write the fractions and match fractions in Column I with the equivalent fractions in Column II.

Solution:
(i) (b)
(ii) (c)
(iii) (a)
(iv) (d)
3. Replace ☐ in each of the following by the correct number:
(i) 2/7 = 6/ ☐
(ii) 5/8 = 10/☐
(iii) 4/5 = ☐/20
(iv) 45/60 = 15/ ☐
(v) 18/24 = ☐/4
Solution:
(i) 2/7 = 6/21
(ii) 5/8 = 10/16
(iii) 4/5 = 16/20
(iv) 45/60 = 15/20
(v) 18/24 =3/4
4. Find the equivalent fraction of 3/5, having:
(i) numerator 9
(ii) denominator 30
(iii) numerator 21
(iv) denominator 40
Solution:
(i) The given fraction = 3/5
By considering numerator = 9
We know that 3 × 3 = 9
Multiply the numerator and denominator of the fraction by 3
3/5 × 3/3 = 9/15
(ii) The given fraction = 3/5
By considering denominator = 30
We know that 5 × 6 = 30
Multiply the numerator and denominator of the fraction by 6
3/5 × 6/6 = 18/30
(iii) The given fraction = 3/5
By considering numerator = 21
We know that 3 × 7 = 21
Multiply the numerator and denominator of the fraction by 7
3/5 × 7/7 = 21/35
(iv) The given fraction = 3/5
By considering denominator = 40
We know that 5 × 8 = 40
Multiply the numerator and denominator of the fraction by 8
3/5 × 8/8 = 24/40
5. Find the fraction equivalent to 45/60, having:
(i) numerator 15
(ii) denominator 4
(iii) denominator 240
(iv) numerator 135
Solution:
(i) The given fraction = 45/60
By considering numerator = 15
We know that 45 ÷ 3 = 15
Dividing the numerator and denominator of the fraction by 3
45/60 ÷ 3/3 = 15/20
(ii) The given fraction = 45/60
By considering denominator = 4
We know that 60 ÷ 15 = 4
Dividing the numerator and denominator of the fraction by 15
45/60 ÷ 15/15 = 3/4
(iii) The given fraction = 45/60
By considering denominator = 240
We know that 60 × 4 = 240
Multiply the numerator and denominator of the fraction by 4
45/60 × 4/4 = 180/240
(iv) The given fraction = 45/60
By considering numerator = 135
We know that 45 × 3 = 135
Dividing the numerator and denominator of the fraction by 3
45/60 × 3/3 = 135/180
6. Find the fraction equivalent of 35/42, having:
(i) numerator 15
(ii) denominator 18
(iii) denominator 30
(iv) numerator 30
Solution:
The given fraction = 35/42
In order to reduce the fraction, divide the numerator and denominator by the HCF of 35 and 42
We get
35/42 ÷ 7/7 = 5/6
(i) So the fraction = 5/6
By considering numerator = 15
We know that 5 × 3 = 15
Multiply the numerator and denominator of the fraction by 3
5/6 × 3/3 = 15/18
(ii) So the fraction = 5/6
By considering denominator = 18
We know that 6 × 3 = 18
Multiply the numerator and denominator of the fraction by 3
5/6 × 3/3 = 15/18
(iii) So the fraction = 5/6
By considering denominator = 30
We know that 6 × 5 = 30
Multiply the numerator and denominator of the fraction by 5
5/6 × 5/5 = 25/30
(iv) So the fraction = 5/6
By considering numerator = 30
We know that 5 × 6 = 30
Multiply the numerator and denominator of the fraction by 6
5/6 × 6/6 = 30/36
7. Check whether the given fractions are equivalent:
(i) 5/9, 30/54
(ii) 2/7, 16/42
(iii) 7/13, 5/11
(iv) 4/11, 32/88
(v) 3/10, 12/50
(vi) 9/27, 25/75
Solution:
(i) We know that
5/9 × 6/6 = 30/54
Therefore, 5/9 is equivalent to 30/54.
(ii) We know that
2/7 × 8/8 = 16/56
Therefore, 2/7 is not equivalent to 16/42.
(iii) We know that
7/13 × 5/5 = 35/65
The same way
5/11 × 7/7 = 35/77
Therefore, 7/13 is not equivalent to 5/11.
(iv) We know that
4/11 × 8/8 = 32/88
Therefore, 4/11 is equivalent to 32/88.
(v) We know that
3/10 × 4/4 = 12/40
Therefore, 3/10 is not equivalent to 12/50.
(vi) We know that
9/27 = 1/3 and 25/75 = 1/3
Therefore, 9/27 is equivalent to 25/75.
8. Match the equivalent fractions and write another 2 for each:
(i) 250/400 (a) 2/3
(ii) 180/200 (b) 2/5
(iii) 660/990 (c) ½
(iv) 180/360 (d) 5/8
(v) 220/550 (e) 9/10
Solution:
(i) 250/400
By dividing numerator and denominator by HCF of 250 and 400
= (250/50)/ (400/ 50) = 5/8
So the match is (d)
(ii) 180/200
By dividing numerator and denominator by HCF of 180 and 200
= (180/20)/ (200/20) = 9/10
So the match is (e)
(iii) 660/990
By dividing numerator and denominator by HCF of 660 and 990
= (660/30)/ (990/90) = 2/3
So the match is (a)
(iv) 180/360
By dividing numerator and denominator by HCF of 180 and 360
= (180/180)/ (360/180) = ½
So the match is (c)
(v) 220/550
By dividing numerator and denominator by HCF of 220 and 550
= (220/11)/ (550/11) = 2/5
So the match is (b)
9. Write some equivalent fractions which contain all digits from 1 to 9 once only.
Solution:
The equivalent fractions which contain all digits from 1 to 9 once only are
2/6 = 3/9 = 58/174, 2/4 = 3/6 = 79/158
10. Ravish had 20 pencils, Sikha had 50 pencils and Priya had 80 pencils. After 4 months, Ravish used up 10 pencils, Shikha used up 25 pencils and Priya used up 40 pencils. What fraction did each use up? Check if each has used up an equal fraction of their pencils?
Solution:
Number of pencils Ravish had = 20
Number of pencils Ravish used = 10
By dividing the numerator and denominator by HCF of 10 and 20
We get the fraction of pencils used = (10 ÷ 10)/ (20 ÷ 10) = 1/2
Number of pencils Shikha had = 50
Number of pencils used by Shikha = 25
By dividing the numerator and denominator by HCF of 25 and 50
We get the fraction of pencils used = (25 ÷ 25)/ (50 ÷ 25) = 1/2
Number of pencils Priya had = 80
Number of pencils used by Priya = 40
By dividing the numerator and denominator by HCF of 40 and 80
We get the fraction of pencils used = (40 ÷ 40)/ (80 ÷ 40) = 1/2
Yes, each has used up an equal fraction of their pencils.
Exercise 6.6 PAGE: 6.19
Reduce each of the following fractions to its lowest term (simplest form):
1. (i) 40/75
(ii) 42/28
(iii) 12/52
(iv) 40/72
(v) 80/24
(vi) 84/56
Solution:
(i) 40/75
We know that
Factors of 40 are
1, 2, 4, 5, 8, 10, 20 and 40
Factors of 75 are
1, 3, 5, 15 and 75
So the common factors are 1 and 5
We get HCF = 5
By dividing numerator and denominator by 5
40/75 ÷ 5/5 = 8/15
Hence, the simplest form of 40/75 is 8/15.
(ii) 42/28
We know that
Factors of 42 are
1, 2, 3, 6, 7, 14, 21 and 42
Factors of 28 are
1, 2, 4, 7, 14 and 28
So the common factors are 1, 2 and 4
We get HCF = 4
By dividing numerator and denominator by 4
42/28 ÷ 4/4 = 3/2
Hence, the simplest form of 42/28 is 3/2.
(iii) 12/52
We know that
Factors of 12 are
1, 2, 3, 6 and 12
Factors of 52 are
1, 2, 4, 13, 26 and 52
So the common factors are 1, 2 and 4
We get HCF = 4
By dividing numerator and denominator by 4
12/52 ÷ 4/4 = 3/13
Hence, the simplest form of 12/52 is 3/13.
(iv) 40/72
We know that
Factors of 40 are
1, 2, 4, 5, 8, 10, 20 and 40
Factors of 72 are
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72
So the common factors are 1, 2, 4 and 8
We get HCF = 8
By dividing numerator and denominator by 8
40/72 ÷ 8/8 = 5/9
Hence, the simplest form of 40/72 is 5/9.
(v) 80/24
We know that
Factors of 80 are
1, 2, 4, 5, 8, 10, 16, 20, 40 and 80
Factors of 24 are
1, 2, 3, 4, 6, 8, 12 and 24
So the common factors are 1, 2, 4 and 8
We get HCF = 8
By dividing numerator and denominator by 8
80/24 ÷ 8/8 = 10/3
Hence, the simplest form of 80/24 is 10/3.
(vi) 84/56
We know that
Factors of 84 are
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84
Factors of 56 are
1, 2, 4, 7, 8, 14, 28 and 56
So the common factors are 1, 2, 4, 7, 14 and 28
We get HCF = 28
By dividing numerator and denominator by 28
84/56 ÷ 28/28 = 3/2
Hence, the simplest form of 84/56 is 3/2.
2. Simplify each of the following to its lowest term:
(i) 75/80
(ii) 52/76
(iii) 84/98
(iv) 68/17
(v) 150/50
(vi) 162/108
Solution:
(i) 75/80
We know that
Factors of 75 are
1, 3, 5, 15, 25 and 75
Factors of 80 are
1, 2, 4, 5, 8, 10, 12, 16, 20, 40 and 80
So the common factors are 1 and 5
We get HCF = 5
By dividing numerator and denominator by 5
75/80 ÷ 5/5 = 15/16
Hence, the simplest form of 75/80 is 15/16.
(ii) 52/76
We know that
Factors of 52 are
1, 2, 4, 13, 26 and 52
Factors of 76 are
1, 2, 4, 19, 38 and 76
So the common factors are 1, 2 and 4
We get HCF = 4
By dividing numerator and denominator by 4
52/76 ÷ 4/4 = 13/19
Hence, the simplest form of 52/76 is 13/19.
(iii) 84/98
We know that
Factors of 84 are
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84
Factors of 98 are
1, 2, 7, 14, 49 and 98
So the common factors are 1, 2, 7 and 14
We get HCF = 14
By dividing numerator and denominator by 14
84/98 ÷ 14/14 = 6/7
Hence, the simplest form of 84/98 is 6/7.
(iv) 68/17
We know that
Factors of 68 are
1, 2, 4, 17, 34 and 68
Factors of 17 are
1 and 17
So the common factors are 1 and 17
We get HCF = 17
By dividing numerator and denominator by 5
68/17 ÷ 17/17 = 4/1
Hence, the simplest form of 68/17 is 4/1.
(v) 150/50
We know that
Factors of 150 are
1, 2, 3, 5, 6, 10, 15, 25, 50 and 150
Factors of 50 are
1, 2, 5, 10, 25 and 50
So the common factors are 1, 2, 5, 10, 25 and 50
We get HCF = 50
By dividing numerator and denominator by 50
150/50 ÷ 50/50 = 3/1
Hence, the simplest form of 150/50 is 3/1.
(vi) 162/108
We know that
Factors of 162 are
1, 2, 3, 6, 9, 18, 27, 54, 81 and 162
Factors of 108 are
1, 2, 3, 4, 6, 9, 12, 18, 27 and 54
So the common factors are 1, 2, 3, 6, 9, 18, 27 and 54
We get HCF = 54
By dividing numerator and denominator by 54
162/108 ÷ 54/54 = 3/2
Hence, the simplest form of 162/108 is 3/2.
Exercise 6.7 page: 6.24
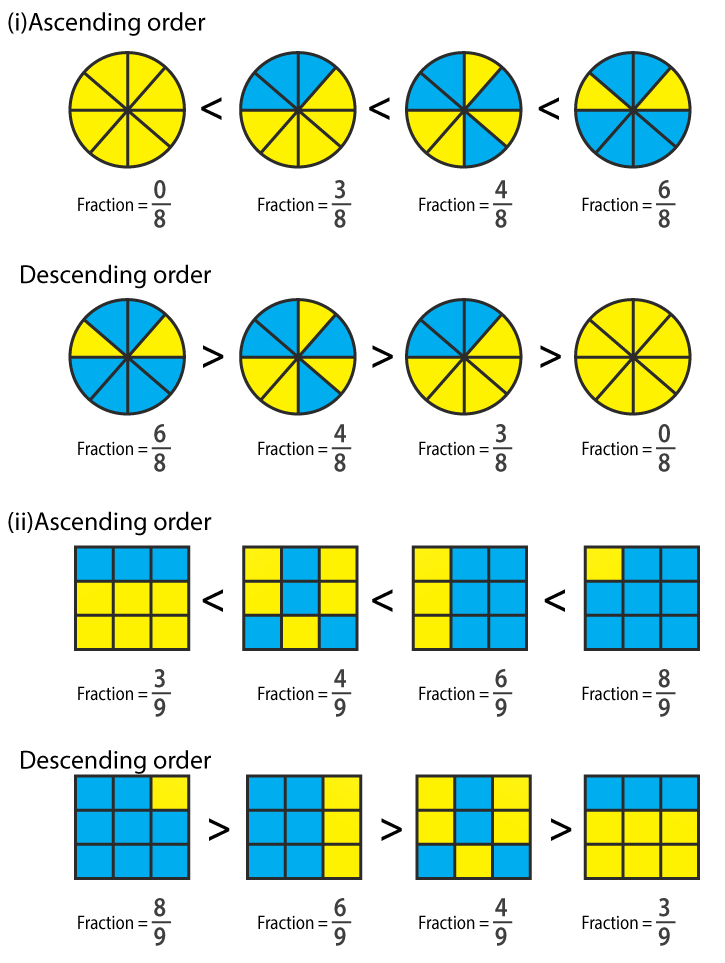
1. Write each fraction. Arrange them in ascending and descending order using correct sign <, =, > between the fractions:

Solution:

2. Mark 2/6, 4/6, 8/6 and 6/6 on the number line and put appropriate signs between fractions given below:
(i) 5/6 …….. 2/6
(ii) 3/6 ……. 0/6
(iii) 1/6 …… 6/6
(iv) 8/6 …… 5/6
Solution:

(i) We know that
5/6 > 2/6 as 5 > 2 and the denominator is same.
(ii) We know that
3/6 > 0/6 as 3 > 0 and the denominator is same.
(iii) We know that
1/6 < 6/6 as 6 > 1 and the denominator is same.
(iv) We know that
8/6 > 5/6 as 8 > 5 and the denominator is same.
3. Compare the following fractions and put an appropriate sign:
(i) 3/6 …… 5/6
(ii) 4/5 …… 0/5
(iii) 3/20 …… 4/20
(iv) 1/7 ……. 1/4
Solution:
(i) We know that
3/6 < 5/6 as 3 < 5 and the denominator is same.
(ii) We know that
4/5 > 0/5 as 4 > 0 and the denominator is same.
(iii) We know that
3/20 < 4/20 as 3 < 4 and the denominator is same.
(iv) We know that
1/7 < 1/4 as 7 > 4 and the fraction having smaller denominator is larger.
4. Compare the following fractions using the symbol > or <: strong="">
(i) 6/7 and 6/11
(ii) 3/7 and 5/7
(iii) 2/3 and 8/12
(iv) 1/5 and 4/15
(v) 8/3 and 8/13
(vi) 4/9 and 15/8
Solution:
(i) We know that
6/7 > 6/11 as the fraction having smaller denominator is larger.
(ii) We know that
3/7 < 5/7 as 3 < 5 and the denominator is same.
(iii) We know that
8/12 = (2 × 2 × 2)/ (2 × 2 × 3) = 2/3
Hence, 2/3 = 8/12
(iv) We know that
1/5 = (1/ 5) × (3/3) = 3/15 which is lesser than 4/15
Hence, 1/5 < 4/15
(v) We know that
8/3 < 8/13 as the fraction having smaller value of denominator is larger.
(vi) We know that
4/9 = (4/9) × (8/8) = 32/72
15/8 = (15/8) × (9/9) = 135/72
So we get 32/72 < 135/72
Hence, 4/9 < 15/8.
5. The following fractions represent just three different numbers. Separate them in to three groups of equal fractions by changing each one to its simplest form:
(i) 2/12
(ii) 3/15
(iii) 8/50
(iv) 16/100
(v) 10/60
(vi) 15/75
(vii) 12/60
(viii) 16/96
(ix) 12/75
(x) 12/72
(xi) 3/18
(xii) 4/25
Solution:
(i) 2/12
We know that HCF of 2 and 12 = 2
By dividing numerator and denominator by HCF of 2 and 12
2/12 ÷ 2/2 = 1/6
(ii) 3/15
We know that HCF of 3 and 15 = 3
By dividing numerator and denominator by HCF of 3 and 15
3/15 ÷ 3/3 = 1/5
(iii) 8/50
We know that HCF of 8 and 50 = 2
By dividing numerator and denominator by HCF of 8 and 50
8/50 ÷ 2/2 = 4/25
(iv) 16/100
We know that HCF of 16 and 100 = 4
By dividing numerator and denominator by HCF of 16 and 100
16/100 ÷ 4/4 = 4/25
(v) 10/60
We know that HCF of 10 and 60 = 10
By dividing numerator and denominator by HCF of 10 and 60
10/60 ÷ 10/10 = 1/6
(vi) 15/75
We know that HCF of 15 and 75 = 15
By dividing numerator and denominator by HCF of 15 and 75
15/75 ÷ 15/15 = 1/5
(vii) 12/60
We know that HCF of 2 and 12 = 12
By dividing numerator and denominator by HCF of 2 and 12
12/60 ÷ 12/12 = 1/5
(viii) 16/96
We know that HCF of 16 and 96 = 16
By dividing numerator and denominator by HCF of 16 and 96
16/96 ÷ 16/16 = 1/6
(ix) 12/75
We know that HCF of 12 and 75 = 3
By dividing numerator and denominator by HCF of 12 and 75
12/75 ÷ 3/3 = 4/25
(x) 12/72
We know that HCF of 12 and 72 = 12
By dividing numerator and denominator by HCF of 12 and 72
12/72 ÷ 12/12 = 1/6
(xi) 3/18
We know that HCF of 3 and 18 = 3
By dividing numerator and denominator by HCF of 3 and 18
3/18 ÷ 3/3 = 1/6
(xii) 4/25
We know that HCF of 4 and 25 = 1
By dividing numerator and denominator by HCF of 4 and 25
4/25 ÷ 1/1 = 4/25
Three groups of equal fractions: 2/12, 10/60, 16/96, 12/72, 3/18, 3/15, 15/75, 12/60, 8/50, 16/100, 12/75, 4/25
6. Isha read 25 pages of a book containing 100 pages. Nagma read ½ of the same book. Who read less?
Solution:
No. of pages in the book = 100
We know that
Fraction of book Isha read = (25/100) ÷ (25/25) = 1/4 by dividing both numerator and denominator by HCF of 25 and 100
So the fraction of book Nagma read = 1/2
By comparing 1/4 and 1/2 we get the LCM of 4 and 2 = 4
Now convert the fraction into equivalent fraction having denominator as 4
1 × 1/4 × 1 and 1 × 2/2 × 2/14 and 1/4 = 2/4
Hence, Isha read less.
7. Arrange the following fractions in the ascending order:
(i) 2/9, 7/9, 3/9, 4/9, 1/9, 6/9, 5/9
(ii) 7/8, 7/25, 7/11, 7/18, 7/10
(iii) 37/47, 37/50, 37/100, 37/1000, 37/85, 37/41
(iv) 3/5, 1/5, 4/5, 2/5
(v) 2/5, 3/4, 1/2, 3/5
(vi) 3/8, 3/12. 3/6, 3/4
(vii) 4/6, 3/8, 6/12, 5/16
Solution:
(i) 2/9, 7/9, 3/9, 4/9, 1/9, 6/9, 5/9 can be written in ascending order as
1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9
(ii) 7/8, 7/25, 7/11, 7/18, 7/10 can be written in ascending order as
7/25, 7/18, 7/11, 7/10, 7/8
(iii) 37/47, 37/50, 37/100, 37/1000, 37/85, 37/41 can be written in ascending order as
37/1000, 37/100, 37/85, 37/50, 37/47, 37/41
(iv) 3/5, 1/5, 4/5, 2/5 can be written in ascending order as
1/5, 2/5, 3/5, 4/5
(v) 2/5, 3/4, 1/2, 3/5 can be written in ascending order as
2/5, 1/2, 3/5, 3/4
(vi) 3/8, 3/12, 3/6, 3/4 can be written in ascending order as
3/12, 3/8, 3/6, 3/4
(vii) 4/6, 3/8, 6/12, 5/16 can be written in ascending order as
5/16, 3/8, 6/12, 4/6
8. Arrange in descending order in each of the following using the symbol >:
(i) 8/17, 8/9, 8/5, 8/13
(ii) 5/9, 3/12, 1/3, 4/15
(iii) 2/7, 11/35, 9/14, 13/28
Solutions:
(i) 8/17, 8/9, 8/5, 8/13 can be written in the descending order as
8/5 > 8/9 > 8/13 > 8/17
(ii) 5/9, 3/12, 1/3, 4/15 can be written in the descending order as
5/9 > 1/3 > 3/12 > 4/15
(iii) 2/7, 11/35, 9/14, 13/28 can be written in the descending order as
9/14 > 13/28 > 11/35 > 2/7
9. Find answers to the following. Write and indicate how you solved them.
(i) Is 5/9 equal to 4/5?
(ii) Is 9/16 equal to 5/9?
(iii) Is 4/5 equal to 16/20?
(iv) Is 1/15 equal to 4/30?
Solution:
(i) No. We know that 5 × 5 ≠ 9 × 4
(ii) No. We know that 9 × 9 ≠ 16 × 5
(iii) Yes. We know that 4 × 20 = 16 × 5
(iv) No. We know that 1 × 30 = 15 × 4
Exercise 6.8 PAGE: 6.29
1. Write these fractions appropriately as additions or subtractions:

Solution:
(i) It can be written as
1/5 + 2/5 = 3/5
(ii) It can be written as
3/6 + 2/6 = 5/6
2. Solve:
(i) 5/12 + 1/12
(ii) 3/15 + 7/15
(iii) 3/22 + 7/22
(iv) 1/4 + 0/4
(v) 4/13 + 2/13 + 1/13
(vi) 0/15 + 2/15 + 1/15
(vii) 7/31 – 4/31 + 9/31
(viii) 3 2/7 + 1/7 – 2 3/7
(ix) 2 1/3 – 1 2/3 + 4 1/3
(x) 1 – 2/3 + 7/3
(xi) 16/7 – 5/7 + 9/7
Solution:
(i) 5/12 + 1/12
It can be written as
5/ 12 + 1/12 = (5 + 1)/ 12
On further calculation
5/ 12 + 1/12 = 6/12 = 1/2
(ii) 3/15 + 7/15
It can be written as
3/15 + 7/15 = (3 + 7)/ 15
On further calculation
3/15 + 7/15 = 10/15 = 2/3
(iii) 3/22 + 7/22
It can be written as
3/22 + 7/22 = (3 + 7)/ 22
On further calculation
3/22 + 7/22 = 10/22 = 5/11
(iv) 1/4 + 0/4
It can be written as
1/4 + 0/4 = (1 + 0)/4
On further calculation
1/4 + 0/4 = ¼
(v) 4/13 + 2/13 + 1/13
It can be written as
4/13 + 2/13 + 1/13 = (4 + 2 + 1)/ 13
On further calculation
4/13 + 2/13 + 1/13 = 7/13
(vi) 0/15 + 2/15 + 1/15
It can be written as
0/15 + 2/15 + 1/15 = (0 + 2 + 1)/ 15
On further calculation
0/15 + 2/15 + 1/15 = 3/15 = 1/5
(vii) 7/31 – 4/31 + 9/31
It can be written as
7/31 – 4/31 + 9/31 = (7 – 4 + 9)/ 31
On further calculation
7/31 – 4/31 + 9/31 = 12/31
(viii) 3 2/7 + 1/7 – 2 3/7
It can be written as
3 2/7 + 1/7 – 2 3/7 = (23 + 1 – 17)/ 7
On further calculation
3 2/7 + 1/7 – 2 3/7 = 7/7 = 1
(ix) 2 1/3 – 1 2/3 + 4 1/3
It can be written as
2 1/3 – 1 2/3 + 4 1/3 = (7 – 5 + 13)/ 3
On further calculation
2 1/3 – 1 2/3 + 4 1/3 = 15/3 = 5
(x) 1 – 2/3 + 7/3
It can be written as
1 – 2/3 + 7/3 = (3 – 2 + 7)/3
On further calculation
1 – 2/3 + 7/3 = 8/3
(xi) 16/7 – 5/7 + 9/7
It can be written as
16/7 – 5/7 + 9/7 = (16 – 5 + 9)/ 7
On further calculation
16/7 – 5/7 + 9/7 = 20/7
3. Shikha painted 1/5 of the wall space in her room. Her brother Ravish helped and painted 3/5 of the wall space. How much did they paint together? How much the room is left unpainted?
Solution:
Fraction of wall space painted by Shikha = 1/5
Fraction of wall space painted by Ravish = 3/5
So the wall space painted by both = 1/5 + 3/5
= (1+3)/5
= 4/5
We get the unpainted space = (5 – 4)/ 5 = 1/5
Therefore, Shikha and Ravish painted 4/5 of the wall space together and the room space left unpainted is 1/5.
4. Ramesh bought 2 ½ kg sugar whereas Rohit bought 3 ½ kg of sugar. Find the total amount of sugar bought by both of them.
Solution:
Sugar bought by Ramesh = 2 ½ kg
It can be written as
Sugar bought by Ramesh = ((2 × 2) + 1)/ 2 = 5/2 kg
Sugar bought by Rohit = 3 ½ kg
It can be written as
Sugar bought by Rohit = ((2 × 3) + 1)/ 2 = 7/2 kg
So the total sugar bought by both of them = Sugar bought by Ramesh + Sugar bought by Rohit
By substituting the values
Total sugar bought by both of them = 5/2 + 7/2 = 12/2 = 6kg
Therefore, the total amount of sugar bought by both of them is 6kg.
5. The teacher taught 3/5 of the book, Vivek revised 1/5 more on his own. How much does he still have to revise?
Solution:
We know that
Fraction of book teacher taught = 3/5
Fraction of book Vivek revised = 1/5
So the fraction of book Vivek still have to revise = 3/5 – 1/5
= (3 – 1)/ 5
= 2/5
Hence, Vivek still have to revise 2/5 of the book.
6. Amit was given 5/7 of a bucket of oranges. What fraction of oranges was left in the basket?
Solution:
We know that
Fraction of oranges Amit has = 5/7
So the fraction of oranges left in the basket = 1 – 5/7
= (7 – 5)/ 7
= 2/7
Hence, the fraction of oranges left in the basket is 2/7.
7. Fill in the missing fractions:
(i) 7/10 – ☐ = 3/10
(ii) ☐ – 3/21 = 5/21
(iii) ☐ – 3/6 = 3/6
(iv) ☐ – 5/27 = 12/27
Solution:
(i) 7/10 – ☐ = 3/10
It can be written as
7/10 – 3/10 = ☐
We get
(7 – 3)/ 10 = 2/5
(ii) ☐ – 3/21 = 5/21
It can be written as
☐ = 5/21 + 3/21
We get
(5 + 3)/ 21 = 8/21
(iii) ☐ – 3/6 = 3/6
It can be written as
☐ = 3/6 + 3/6
We get
(3 + 3)/ 6 = 6/6 = 1
(iv) ☐ – 5/27 = 12/27
It can be written as
☐ = 12/27 + 5/27
We get
(12 + 5)/ 27 = 17/27
Exercise 6.9 page: 6.35
1. Add:
(i) 3/4 and 5/6
(ii) 7/10 and 2/15
(iii) 8/13 and 2/3
(iv) 4/5 and 7/15
Solution:
(i) 3/4 and 5/6
It can be written as
3/4 + 5/6
We know that the LCM of 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(3 × 3)/ (4 × 3)] + [(5 × 2)/ (6 × 2)]
On further calculation
= 9/12 + 10/ 12
We get
= (9 + 10)/ 12 = 19/12
(ii) 7/10 and 2/15
It can be written as
7/10 + 2/15
We know that the LCM of 10 and 15 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(7 × 3)/ (10 × 3)] + [(2 × 2)/ (15 × 2)]
On further calculation
= 21/30 + 4/ 30
We get
= (21 + 4)/ 30 = 25/30 = 5/6
(iii) 8/13 and 2/3
It can be written as
8/13 + 2/3
We know that the LCM of 13 and 3 is 39
In order to convert fraction into equivalent fraction having 39 as denominator
= [(8 × 3)/ (13 × 3)] + [(2 × 13)/ (3 × 13)]
On further calculation
= 24/39 + 26/39
We get
= (24 + 26)/ 39 = 50/39
(iv) 4/5 and 7/15
It can be written as
4/5 + 7/15
We know that the LCM of 5 and 15 is 1
In order to convert fraction into equivalent fraction having 15 as denominator
= [(4 × 3)/ (5 × 3)] + [(7 × 1)/ (15 × 1)]
On further calculation
= 12/15 + 7/ 15
We get
= (12 + 7)/ 15 = 19/15
2. Subtract:
(i) 2/7 from 19/21
(ii) 21/25 from 18/20
(iii) 7/16 from 2
(iv) 4/15 from 2 1/5
Solution:
(i) 2/7 from 19/21
It can be written as
19/21 – 2/7
We know that LCM of 21 and 7 is 21
In order to convert fraction into equivalent fraction having 21 as denominator
= [(19 × 1)/ (21 × 1)] – [(2 × 3)/ (7 × 3)]
On further calculation
= 19/21 – 6/21
We get
= (19 – 6)/21 = 13/21
(ii) 21/25 from 18/20
It can be written as
18/20 – 21/25
We know that LCM of 20 and 25 is 100
In order to convert fraction into equivalent fraction having 100 as denominator
= [(18 × 5)/ (20 × 5)] – [(21 × 4)/ (25 × 4)]
On further calculation
= 90/100 – 84/100
We get
= (90 – 84)/100 = 6/100 = 3/50
(iii) 7/16 from 2
It can be written as
2/1 – 7/16
We know that LCM of 1 and 16 is 16
In order to convert fraction into equivalent fraction having 16 as denominator
= [(16 × 2)/ (16 × 1)] – [(7 × 1)/ (16 × 1)]
On further calculation
= 32/16 – 7/16
We get
= (32 – 7)/16 = 25/16
(iv) 4/15 from 2 1/5
It can be written as
11/5 – 4/15
We know that LCM of 5 and 15 is 15
In order to convert fraction into equivalent fraction having 15 as denominator
= [(11 × 3)/ (5 × 3)] – [(4 × 1)/ (15 × 1)]
On further calculation
= 33/15 – 4/15
We get
= (33 – 4)/15 = 29/15
3. Find the difference of:
(i) 13/24 and 7/16
(ii) 5/18 and 4/15
(iii) 1/12 and 3/4
(iv) 2/3 and 6/7
Solution:
(i) 13/24 and 7/16
It can be written as
13/24 – 7/16
We know that LCM of 24 and 16 is 48
In order to convert fraction into equivalent fraction having 48 as denominator
= [(13 × 2)/ (24 × 2)] – [(7 × 3)/ (16 × 3)]
On further calculation
= 26/48 – 21/48
We get
= (26 – 21)/48 = 5/48
(ii) 5/18 and 4/15
It can be written as
5/18 – 4/15
We know that LCM of 18 and 15 is 90
In order to convert fraction into equivalent fraction having 90 as denominator
= [(5 × 5)/ (18 × 5)] – [(4 × 6)/ (15 × 6)]
On further calculation
= 25/90 – 24/90
We get
= (25 – 24)/90 = 1/90
(iii) 1/12 and 3/4
It can be written as
3/4 – 1/12
We know that LCM of 4 and 12 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(3 × 3)/ (4 × 3)] – [(1 × 1)/ (12 × 1)]
On further calculation
= 9/12 – 1/12
We get
= (9 – 1)/12 = 8/12 = 2/3
(iv) 2/3 and 6/7
It can be written as
6/7 – 2/3
We know that LCM of 7 and 3 is 21
In order to convert fraction into equivalent fraction having 48 as denominator
= [(6 × 3)/ (7 × 3)] – [(2 × 7)/ (3 × 7)]
On further calculation
= 18/21 – 14/21
We get
= (18 – 14)/21 = 4/21
4. Subtract as indicated:
(i) 8/3 – 5/9
(ii) 4 2/5 – 2 1/5
(iii) 5 6/7 – 2 2/3
(iv) 4 3/4 – 2 1/6
Solution:
(i) 8/3 – 5/9
It can be written as
8/3 – 5/9
We know that LCM of 3 and 9 is 9
In order to convert fraction into equivalent fraction having 9 as denominator
= [(8 × 3)/ (3 × 3)] – [(5 × 1)/ (9 × 1)]
On further calculation
= 24/9 – 5/9
We get
= (24 – 5)/9 = 19/9
(ii) 4 2/5 – 2 1/5
It can be written as
22/5 – 11/5
We get
= (22 – 11)/5 = 11/5
(iii) 5 6/7 – 2 2/3
It can be written as
41/7 – 8/3
We know that LCM of 7 and 3 is 21
In order to convert fraction into equivalent fraction having 21 as denominator
= [(41 × 3)/ (7 × 3)] – [(8 × 7)/ (3 × 7)]
On further calculation
= 123/21 – 56/21
We get
= (123 – 56)/21 = 67/21
(iv) 4 3/4 – 2 1/6
It can be written as
19/4 – 13/6
We know that LCM of 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(19 × 3)/ (4 × 3)] – [(13 × 2)/ (6 × 2)]
On further calculation
= 57/21 – 26/21
We get
= (57 – 26)/21 = 31/12
5. Simplify:
(i) 2/3 + 3/4 + 1/2
(ii) 5/8 + 2/5 + 3/4
(iii) 3/10 + 7/15 + 3/5
(iv) 3/4 + 7/16 + 5/8
(v) 4 2/3 + 3 1/4 + 7 1/2
(vi) 7 1/3 + 3 2/3 + 5 1/6
(vii) 7 + 7/4 + 5 1/6
(viii) 5/6 + 3 + 3/4
(ix) 7/18 + 5/6 + 1 1/12
Solution:
(i) 2/3 + 3/4 + 1/2
We know that the LCM of 3, 4 and 2 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(2 × 4)/ (3 × 4)] + [(3 × 3)/ (4 × 3)] + [(1 × 6)/ (2 × 6)]
On further calculation
= 8/12+ 9/12 + 6/12
We get
= (8 + 9 + 6)/ 12 = 23/12
(ii) 5/8 + 2/5 + 3/4
We know that the LCM of 8, 5 and 4 is 40
In order to convert fraction into equivalent fraction having 40 as denominator
= [(5 × 5)/ (8 × 5)] + [(2 × 8)/ (5 × 8)] + [(3 × 10)/ (4 × 10)]
On further calculation
= 25/40 + 16/40 + 30/40
We get
= (25 + 16 + 30)/ 40 = 71/40
(iii) 3/10 + 7/15 + 3/5
We know that the LCM of 10, 15 and 5 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(3 × 3)/ (10 × 3)] + [(7 × 2)/ (15 × 2)] + [(3 × 6)/ (5 × 6)]
On further calculation
= 9/30+ 14/30 + 18/30
We get
= (9 + 14 + 18)/ 30 = 41/30
(iv) 3/4 + 7/16 + 5/8
We know that the LCM of 4, 16 and 8 is 16
In order to convert fraction into equivalent fraction having 16 as denominator
= [(3 × 4)/ (4 × 4)] + [(7 × 1)/ (16 × 1)] + [(5 × 2)/ (8 × 2)]
On further calculation
= 12/16 + 7/16 + 10/16
We get
= (12 + 7 + 10)/ 16 = 29/16
(v) 4 2/3 + 3 1/4 + 7 1/2
It can be written as
14/3 + 13/4 + 15/2
We know that the LCM of 3, 4 and 2 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(14 × 4)/ (3 × 4)] + [(13 × 3)/ (4 × 3)] + [(15 × 6)/ (2 × 6)]
On further calculation
= 56/12 + 39/12 + 90/12
We get
= (56 + 39 + 90)/ 12 = 185/12
(vi) 7 1/3 + 3 2/3 + 5 1/6
It can be written as
22/3 + 11/3 + 31/6
We know that the LCM of 3, 3 and 6 is 6
In order to convert fraction into equivalent fraction having 6 as denominator
= [(22 × 2)/ (3 × 2)] + [(11 × 2)/ (3 × 2)] + [(31 × 1)/ (6 × 1)]
On further calculation
= 44/6 + 22/6 + 31/6
We get
= (44 + 22 + 31)/ 6 = 97/6
(vii) 7 + 7/4 + 5 1/6
It can be written as
7/1 + 7/4 + 31/6
We know that the LCM of 1, 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(7 × 12)/ (1 × 12)] + [(7 × 3)/ (4 × 3)] + [(31 × 2)/ (6 × 2)]
On further calculation
= 84/12 + 21/12 + 62/12
We get
= (84 + 21 + 62)/12 = 167/12
(viii) 5/6 + 3 + 3/4
We know that the LCM of 6, 1 and 4 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(5 × 2)/ (6 × 2)] + [(3 × 12)/ (1 × 12)] + [(3 × 3)/ (4 × 3)]
On further calculation
= 10/12 + 36/12 + 9/12
We get
= (10 + 36 + 9)/ 12 = 55/12
(ix) 7/18 + 5/6 + 1 1/12
It can be written as
7/18 + 5/6 + 13/12
We know that the LCM of 18, 6 and 12 is 36
In order to convert fraction into equivalent fraction having 12 as denominator
= [(7 × 2)/ (18 × 2)] + [(5 × 6)/ (6 × 6)] + [(13 × 3)/ (12 × 3)]
On further calculation
= 14/36 + 30/36 + 39/36
We get
= (14 + 30 + 39)/36 = 83/36
6. Replace ☐ by the correct number:
(i) ☐ – 5/8 = 1/4
(ii) ☐ – 1/5 = 1/2
(iii) 1/2 – ☐ = 1/6
Solution:
(i) ☐ – 5/8 = 1/4
It can be written as
☐ = 1/4 + 5/8
On further calculation
☐ = [(1 × 2)/ (4 × 2)] + [(5 × 1)/ (8 × 1)]
We get
☐ = 2/8 + 5/8
By addition
☐= (2 + 5)/ 8 = 7/8
(ii) ☐ – 1/5 = 1/2
It can be written as
☐ = 1/2 + 1/5
On further calculation
☐ = [(1 × 2)/ (2 × 5)] + [(1 × 5)/ (5 × 2)]
We get
☐ = 2/10 + 5/10
By addition
☐ = (2 + 5)/ 10 = 7/10
(iii) 1/2 – ☐ = 1/6
It can be written as
☐ = 1/2 – 1/6
On further calculation
☐ = [(1 × 3)/ (2 × 3)] – [(1 × 1)/ (6 × 1)]
We get
☐ = 3/6 – 1/6
By addition
☐ = (3 – 1)/ 6 = 2/6 = 1/3
7. Savita bought 2/5 m of ribbon and Kavita 3/4 m of the ribbon. What was the total length of the ribbon they bought?
Solution:
Length of ribbon Savita bought = 2/5 m
Length of ribbon Kavita bought = 3/4 m
So the total length of ribbon they bought = 2/5 + 3/4
We know that the LCM of 5 and 4 is 20
So we get
= [(2 × 4)/ (5 × 4)] + [(3 × 5)/ (4 × 5)]
On further calculation
= 8/20 + 15/20
We get
= (8 + 15)/20 = 23/20 m
Hence, the total length of the ribbon they bought is 23/20 m.
8. Ravish takes 2 1/5 minutes to walk across the school ground. Rahul takes 7/4 minutes to do the same. Who takes less time and by what fraction?
Solution:
Time taken by Ravish to walk across the school ground = 2 1/5 minutes = 11/5 minutes
Time taken by Rahul to walk across the school ground = 7/4 minutes
By comparing 11/5 and 7/4 minutes
We know that LCM of 4 and 5 is 20
In order to convert fraction into equivalent fraction having 20 as denominator
[(11 × 4)/ (5 × 4)], [(7 × 5)/ (4 × 5)]
So we get 44/20 > 35/20
So Rahul takes less time
It can be written as
44/20 – 35/20 = (44 – 35)/20 = 9/20 minutes
Hence, Rahul takes less time by 9/20 minutes.
9. A piece of a wire 7/8 metres long broke into two pieces. One piece was ¼ meter long. How long is the other piece?
Solution:
It is given that
Length of wire = 7/8 m
Length of first piece = 1/4 m
Consider x m as the length of second piece
It can be written as
Length of wire = Length of first piece + Length of second piece
By substituting the values
7/8 = 1/4 + x
On further calculation
x = 7/8 – 1/4
We know that the LCM of 8 and 4 is 8
x = [(7 × 1)/ (8 × 1)] – [(1 × 2)/ (4 × 2)]
We get
x = 7/8 – 2/8
By subtraction
x = (7 – 2)/ 8 = 5/8 m
Hence, the length of second piece of wire is 5/8 m.
10. Shikha and Priya have bookshelves of the same size Shikha’s shelf is 5/6 full of book and Priya’s shelf is 2/5 full. Whose bookshelf is more full? By what fraction?
Solution:
Fraction of Shikha’s shelf filled with books = 5/6
Fraction of Priya’s shelf filled with books = 2/5
We know that LCM of 5 and 6 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(5 × 5)/ (6 × 5)], [(2 × 6)/ (5 × 6)]
So we get 25/30 > 12/30
So Shikha’s shelf is more full.
It can be written as
25/30 – 12/30 = (25 – 12)/ 30 = 13/30
Hence, Shikha’s bookshelf is more full by 13/30.
11. Ravish’s house is 9/10 km from his school. He walked some distance and then took a bus for 1/2km upto the school. How far did he walk?
Solution:
It is given that
Distance of Ravish’s house from his school = 9/10 km
Distance covered by bus = 1/2 km
It can be written as
Distance between house and school = Distance covered by walking + Distance covered by bus
So we get
Distance covered by walking = Distance between house and school – Distance covered by bus
Substituting values
Distance covered by walking = 9/10 – 1/2
We know that LCM of 10 and 2 is 10
In order to convert fraction into equivalent fraction having 10 as denominator
Distance covered by walking = [(9 × 1)/ (10 × 1)] – [(1 × 5)/ (2 × 5)]
We get
Distance covered by walking = 9/10 – 5/10
By subtraction
Distance covered by walking = (9 – 5)/ 10 = 4/10 = 2/5 km
Hence, the distance covered by Ravish by walking is 2/5km.
Objective Type Questions page: 6.36
Mark the correct alternative in each of the following:
1. Which of the following is a proper fraction?
(a) 4/3
(b) 3/4
(c) 13/4
(d) 21/5
(a) 4/3
(b) 3/4
(c) 13/4
(d) 21/5
Solution:
The option (b) is correct answer.
We know that in a proper fraction, the numerator is less than the denominator.
2. Which of the following is an improper fraction?
(a) 1/2
(b) 3/7
(c) 7/3
(d) 3/15
(a) 1/2
(b) 3/7
(c) 7/3
(d) 3/15
Solution:
The option (c) is correct answer.
We know that in an improper fraction, the numerator is more than the denominator.
3. Which of the following is a fraction equivalent of 2/3?
(a) 4/5
(b) 8/6
(c) 10/25
(d) 10/15
(a) 4/5
(b) 8/6
(c) 10/25
(d) 10/15
Solution:
The option (d) is correct answer.
Consider
10/15=2/3
By cross multiplication
10 × 3 = 2 × 15
We get
30 = 30
4. A fraction equivalent to 3/5is
(a) 3+2/5+2
(b) 3-2/5-2
(c) 3×2/5×2
(d) None of these
(a) 3+2/5+2
(b) 3-2/5-2
(c) 3×2/5×2
(d) None of these
Solution:
The option (c) is correct answer.
We know that by dividing the numerator and denominator by 2, we obtain 3/5.
5. If 5/12 is equivalent of x/3, then x =
(a) 5/4
(b) 4/5
(c) 5/3
(d) 3/5
(a) 5/4
(b) 4/5
(c) 5/3
(d) 3/5
Solution:
The option (a) is correct answer.
Consider 5/12 = x/3
By cross multiplication
5 × 3 = 12 × x
So we get
x = (5 × 3)/12 = (5 × 3)/ (4 × 3) = 5/4
6. Which of the following are like fractions?
(a) 3/5, 3/7, 3/11, 3/16
(b) 5/11, 7/11, 15/11, 2/11
(c) 2/3, 3/4,4/5, 6/7
(d) None of these
(a) 3/5, 3/7, 3/11, 3/16
(b) 5/11, 7/11, 15/11, 2/11
(c) 2/3, 3/4,4/5, 6/7
(d) None of these
Solution:
The option (b) is correct answer.
We know that like fractions are the fractions with the same denominator.
7. If 11/4 = 77/x, then x =
(a) 28
(b) 77/28
(c) 44
(d) 308
(a) 28
(b) 77/28
(c) 44
(d) 308
Solution:
The option (a) is correct answer.
11/4 = 77/x
By cross multiplication
11 × x = 77 × 4
x = (77 × 4)/ 11 = (7 × 11 × 4)/ 11
Dividing both the numerator & denominator by 11, we obtain 28.
8. 1/ (2 1/3) +1/ (1 3/4) is equal to
(a) 7/14
(b) 12/49
(c) 4 1/12
(d) None of these
(a) 7/14
(b) 12/49
(c) 4 1/12
(d) None of these
Solution:
The option (d) is correct answer.

9. If 1/3 + 1/2 + 1/x = 4, then x = ?
(a) 5/18
(b) 6/19
(c) 18/5
(d) 24/11
(a) 5/18
(b) 6/19
(c) 18/5
(d) 24/11
Solution:
The option (b) is correct answer.
It is given that
1/3 + ½ + 1/x = 4
On further calculation
1/x = 4 – 1/3 – 1/2
By taking LCM of 3 and 2 as 6
1/x = 24/6 – 2/6 – 3/6
So we get
1/x = (24 – 2 – 3)/ 6 = 19/6
Hence, x = 6/19
10. If 1/2 + 1/x = 2, then x =
(a) 2/5
(b) 5/2
(c) 3/2
(d) 2/3
(a) 2/5
(b) 5/2
(c) 3/2
(d) 2/3
Solution:
The option (d) is correct answer.
It is given that
½ + 1/x = 2
On further calculation
1/x = 2 – 1/2
By taking LCM as 2 we get
1/x = 4/2 – 1/2 = (4 – 1)/2 = 3/2
Hence, x = 2/3
11. Which of the following fractions is the smallest?
1/2,3/7,3/5,4/9
(a) 4/9
(b) 3/5
(c) 3/7
(d) 1/2
1/2,3/7,3/5,4/9
(a) 4/9
(b) 3/5
(c) 3/7
(d) 1/2
Solution:
The option (c) is correct answer.
We know that the LCM of numerator is 12
By converting each fraction to an equivalent fraction having 12 as numerator
1/2 = 1/2 × 12/12 = 12/24
3/7 = 3/7 × 4/4 = 12/28
3/5 = 3/5 × 4/4 = 12/20
4/9 = 4/9 × 3/3 = 12/27
We know that if the numerator is same the fraction having larger denominator is the smallest.
Hence, 3/7 is the smallest fraction.
12. Which of the following fractions is the greatest of all?
7/8, 6/7, 4/5, 5/6
(a) 6/7
(b) 4/5
(c) 5/6
(d) 7/8
(a) 6/7
(b) 4/5
(c) 5/6
(d) 7/8
Solution:
The option (d) is correct answer.
We know that the LCM of 8, 7, 6 and 5 is 840
By converting each fraction to an equivalent fraction having 840 as denominator
7/8 = 7/8 × 105/105 = 735/840
6/7 = 6/7 × 120/120 = 720/840
4/5 = 4/5 × 168/168 = 672/840
5/6 = 5/6 × 140/140 = 700/840
We know that if the denominator is same the fraction having larger numerator is the greatest.
Hence, 7/8 is the greatest fraction.
13. What is the value of a+b/ a−b, If a/b=4?
(a) 3/5
(b) 5/3
(c) 4/5
(d) 5/4
(a) 3/5
(b) 5/3
(c) 4/5
(d) 5/4
Solution:
The option (b) is correct answer.
It is given that a/b = 4
We can write it as a = 4b
By substituting the value of a in a+b/a-b
a+b/a-b = 4b+b/4b-b = 5b/3b
Dividing numerator and denominator by b, the value is 5/3.
14. If a/b = 4/3, then the value of 6a+4b/ 6a-5b is
(a) −1
(b) 3
(c) 4
(d) 5
(a) −1
(b) 3
(c) 4
(d) 5
Solution:
The option (c) is correct answer.
It is given that a/b = 4/3
We can write it as a = 4b/3
By substituting the value of a in 6a+4b/6a-5b

15. If 1/5 – 1/6 = 4/x, then x =
(a) −120
(b) −100
(c) 100
(d) 120
(a) −120
(b) −100
(c) 100
(d) 120
Solution:
The option (d) is correct answer.
It is given that
1/5 – 1/6 = 4/x
LCM of 5 and 6 is 30
4/x = 6/30 – 5/30
On further calculation
4/x = 1/30
So we get
x = 4 (30) = 120
16. The fraction to be added to 6 7/15 to get 8 1/5 is equal to
(a) 11/15
(b) 1 1/15
(c) 44/3
(d) 3/44
(a) 11/15
(b) 1 1/15
(c) 44/3
(d) 3/44
Solution:
The option (b) is correct answer.

17. If 45/60 is equivalent to 3/x, then x =
(a) 5
(b) 4
(c) 6
(d) 20
(a) 5
(b) 4
(c) 6
(d) 20
Solution:
The option (b) is correct answer.
It is given that
45/60 = 3/x
By cross multiplication
45 × x = 3 × 60
It can be written as
x = (3 × 60)/45 = 180/45
Dividing the fraction by HCF
(180 ÷ 45)/(45÷45) = 4
18. A fraction equivalent to 45/105 is
(a) 6/14
(b) 4/7
(c) 5/7
(d) 7/5
(a) 6/14
(b) 4/7
(c) 5/7
(d) 7/5
Solution:
The option (a) is correct answer.
The given fraction is 45/105
By dividing the numerator and denominator with the HCF
(45 ÷ 15)/(105÷15) = 3/7
On further calculation
3/7 = 3/7 × 2/2 = 6/14
19. 5/8 + 3/4 – 7/12 is equal to
(a) 15/24
(b) 17/24
(c) 19/24
(d) 21/24
(a) 15/24
(b) 17/24
(c) 19/24
(d) 21/24
Solution:
The option (c) is correct answer.
The given fraction is
5/8 + 3/4 – 7/12
We know that the LCM is 24
= (5 × 3)/ (8 × 3) + (3 × 6)/ (4 × 6) – (7 × 2)/ (12 × 2)
On further calculation
= 15/24 + 18/24 – 14/24
So we get
= 19/24
20. The correct fraction in the box □ is □ – 5/8=1/4
(a) 6/8
(b) 7/8
(c) 1/2
(d) None of these
(a) 6/8
(b) 7/8
(c) 1/2
(d) None of these
Solution:
The option (b) is correct answer.
The given equation is
□ – 5/8 = 1/4
It can be written as
□ = 1/4 + 5/8
We know that the LCM is 8
□ = 2/8 + 5/8 = 7/8
