NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volumes (Ex 13.6 - Ex 13.8)
Page No: 230Exercise 13.6
Page No: 233
Exercise 13.7
1. Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm
Answer
(i) Radius (r) = 6 cm
Height (h) = 7 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 6 × 6 × 7) cm3
= 264 cm3
(ii) Radius (r) = 3.5 cm
Height (h) = 12 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 3.5 × 3.5 × 12) cm3
= 154 cm3
2. Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm
Answer
(i) Radius (r) = 7 cm
Slant height (l) = 25 cm
Let h be the height of the conical vessel.
∴ h = √l2 - r2
⇒ h = √252 - 72
⇒ h = √576
⇒ h = 24 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 7 × 7 × 24) cm3
= 1232 cm3
Capacity of the vessel = (1232/1000) l = 1.232 l
(i) Height (h) = 12 cm
Slant height (l) = 13 cm
Let r be the radius of the conical vessel.
∴ r = √l2 - h2
⇒ r = √132 - 122
⇒ r = √25
⇒ r = 5 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 5 × 5 × 12) cm3
= (2200/7) cm3
Capacity of the vessel = (2200/7000) l = 11/35 l
3. The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Answer
Height (h) = 15 cm
Volume = 1570 cm3
Let the radius of the base of cone be r cm
∴ Volume = 1570 cm3
⇒ 1/3 πr2h = 1570
⇒ 13 × 3.14 × r2 × 15 = 1570
⇒ r2 = 1570/(3.14×5) = 100
⇒ r = 10
4. If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Answer
Height (h) = 9 cm
Volume = 48π cm3
Let the radius of the base of the cone be r cm
∴ Volume = 48π cm3
⇒ 1/3 πr2h = 48π
⇒ 13 × r2 × 9 = 48
⇒ 3r2 = 48
⇒ r2 = 48/3 = 16
⇒ r = 4
5. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Answer
Diameter of the top of the conical pit = 3.5 m
Radius (r) = (3.5/2) m = 1.75 m
Depth of the pit (h) = 12 m
Volume = 1/3 πr2h
= (13 × 22/7 × 1.75 × 1.75 × 12) m3
= 38.5 m3
1 m3 = 1 kilolitre
Capacity of pit = 38.5 kilolitres.
6. The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone (ii) slant height of the cone
(iii) curved surface area of the cone
Answer
(i) Diameter of the base of the cone = 28 cm
Radius (r) = 28/2 cm = 14 cm
Let the height of the cone be h cm
Volume of the cone = 13πr2h = 9856 cm3
⇒ 1/3 πr2h = 9856
⇒ 1/3 × 22/7 × 14 × 14 × h = 9856
⇒ h = (9856×3)/(22/7 × 14 × 14)
⇒ h = 48 cm
(ii) Radius (r) = 14 m
Height (h) = 48 cm
Let l be the slant height of the cone
l2 = h2 + r2
⇒ l2 = 482 + 142
⇒ l2 = 2304+196
⇒ l2 = 2500
⇒ ℓ = √2500 = 50 cm
(iii) Radius (r) = 14 m
Slant height (l) = 50 cm
Curved surface area = πrl
= (22/7 × 14 × 50) cm2
Exercise 13.7
1. Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm
Answer
(i) Radius (r) = 6 cm
Height (h) = 7 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 6 × 6 × 7) cm3
= 264 cm3
(ii) Radius (r) = 3.5 cm
Height (h) = 12 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 3.5 × 3.5 × 12) cm3
= 154 cm3
2. Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm
Answer
(i) Radius (r) = 7 cm
Slant height (l) = 25 cm
Let h be the height of the conical vessel.
∴ h = √l2 - r2
⇒ h = √252 - 72
⇒ h = √576
⇒ h = 24 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 7 × 7 × 24) cm3
= 1232 cm3
Capacity of the vessel = (1232/1000) l = 1.232 l
(i) Height (h) = 12 cm
Slant height (l) = 13 cm
Let r be the radius of the conical vessel.
∴ r = √l2 - h2
⇒ r = √132 - 122
⇒ r = √25
⇒ r = 5 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 5 × 5 × 12) cm3
= (2200/7) cm3
Capacity of the vessel = (2200/7000) l = 11/35 l
3. The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Answer
Height (h) = 15 cm
Volume = 1570 cm3
Let the radius of the base of cone be r cm
∴ Volume = 1570 cm3
⇒ 1/3 πr2h = 1570
⇒ 13 × 3.14 × r2 × 15 = 1570
⇒ r2 = 1570/(3.14×5) = 100
⇒ r = 10
4. If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Answer
Height (h) = 9 cm
Volume = 48π cm3
Let the radius of the base of the cone be r cm
∴ Volume = 48π cm3
⇒ 1/3 πr2h = 48π
⇒ 13 × r2 × 9 = 48
⇒ 3r2 = 48
⇒ r2 = 48/3 = 16
⇒ r = 4
5. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Answer
Diameter of the top of the conical pit = 3.5 m
Radius (r) = (3.5/2) m = 1.75 m
Depth of the pit (h) = 12 m
Volume = 1/3 πr2h
= (13 × 22/7 × 1.75 × 1.75 × 12) m3
= 38.5 m3
1 m3 = 1 kilolitre
Capacity of pit = 38.5 kilolitres.
6. The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone (ii) slant height of the cone
(iii) curved surface area of the cone
Answer
(i) Diameter of the base of the cone = 28 cm
Radius (r) = 28/2 cm = 14 cm
Let the height of the cone be h cm
Volume of the cone = 13πr2h = 9856 cm3
⇒ 1/3 πr2h = 9856
⇒ 1/3 × 22/7 × 14 × 14 × h = 9856
⇒ h = (9856×3)/(22/7 × 14 × 14)
⇒ h = 48 cm
(ii) Radius (r) = 14 m
Height (h) = 48 cm
Let l be the slant height of the cone
l2 = h2 + r2
⇒ l2 = 482 + 142
⇒ l2 = 2304+196
⇒ l2 = 2500
⇒ ℓ = √2500 = 50 cm
(iii) Radius (r) = 14 m
Slant height (l) = 50 cm
Curved surface area = πrl
= (22/7 × 14 × 50) cm2
= 2200 cm2
7. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Answer
On revolving the ⃤ ABC along the side 12 cm, a right circular cone of height(h) 12 cm, radius(r) 5 cm and slant height(l) 13 cm will be formed.
Volume of solid so obtained = 1/3 πr2h
= (1/3 × π × 5 × 5 × 12) cm3
= 100π cm3
8. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Answer
On revolving the ⃤ ABC along the side 12 cm, a cone of radius(r) 12 cm, height(h) 5 cm, and slant height(l) 13 cm will be formed.
Volume of solid so obtained =1/3 πr2h
= (1/3 × π × 12 × 12 × 5) cm3
= 240π cm3
Ratio of the volumes = 100π/240π = 5/12 = 5:12
9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Answer
Diameter of the base of the cone = 10.5 m
Radius (r) = 10.5/2 m = 5.25 m
Height of the cone = 3 m
Volume of the heap = 1/3 πr2h
= (1/3 × 22/7 × 5.25 × 5.25 × 3) m3
= 86.625 m3
Also,
l2 = h2 + r2
⇒ l2 = 32 + (5.25)2
⇒ l2 = 9 + 27.5625
⇒ l2 = 36.5625
⇒ l = √36.5625 = 6.05 m
Area of canvas = Curve surface area
= πrl = (22/7 × 5.25 × 6.05) m2
= 99.825 m2 (approx)
Page No: 236
Exercise 13.8
1. Find the volume of a sphere whose radius is
(i) 7 cm (ii) 0.63 m
Answer
(i) Radius of the sphere(r) = 7 cm
Therefore, Volume of the sphere = 4/3 πr3
= (4/3 × 22/7 × 7 × 7 × 7) cm3
= 4312/3 cm3
(ii) Radius of the sphere(r) = 0.63 m
Volume of the sphere = 4/3 πr3
= (4/3 × 22/7 × 0.63 × 0.63 × 0.63) m3
= 1.05 m3
2. Find the amount of water displaced by a solid spherical ball of diameter.
(i) 28 cm (ii) 0.21 m
Answer
(i) Diameter of the spherical ball = 28 cm
Radius = 28/2 cm = 14 cm
Amount of water displaced by the spherical ball = Volume
= 4/3 πr3
= (4/3 × 22/7 × 14 × 14 × 14) cm3
= 34496/3 cm3
(ii) Diameter of the spherical ball = 0.21 m
Radius (r) = 0.21/2 m = 0.105 m
Amount of water displaced by the spherical ball = Volume
= 4/3 πr3
= (43×227×0.105×0.105×0.105) m3
= 0.004851 m3
3. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
Answer
Diameter of the ball = 4.2 cm
Radius = (4.2/2) cm = 2.1 cm
Volume of the ball = 4/3 πr3
= (4/3 × 22/7 × 2.1 × 2.1 × 2.1) cm3
= 38.808 cm3
Density of the metal is 8.9g per cm3
Mass of the ball = (38.808 × 8.9) g = 345.3912 g
4. The diameter of the moon is approximately one-fourth of the diameter of the earth.What fraction of the volume of the earth is the volume of the moon?
Answer
Let the diameter of the moon be r
Radius of the moon = r/2
A/q,
Diameter of the earth = 4r
Radius(r) = 4r/2 = 2r
Volume of the moon = v = 4/3 π(r/2)3
= 4/3 πr3 × 1/8
⇒ 8v = 4/3 πr3 --- (i)
Volume of the earth = r3 = 4/3 π(2r)3
= 4/3 πr3× 8
⇒ V/8 = 4/3 πr3 --- (ii)
From (i) and (ii), we have
8v = V/8
⇒ v = 1/64 V
Thus, the volume of the moon is 1/64 of the volume of the earth.
5. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Answer
Diameter of a hemispherical bowl = 10.5 cm
Radius(r) = (10.5/2) cm = 5.25cm
Volume of the bowl = 2/3 πr3
= (2/3 × 22/7 × 5.25 × 5.25 × 5.25) cm3
= 303.1875 cm3
Litres of milk bowl can hold = (303.1875/1000) litres
= 0.3031875 litres (approx.)
6. A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Answer
Internal radius = r = 1m
External radius = R = (1 + 0.1) cm = 1.01 cm
Volume of iron used = External volume – Internal volume
= 2/3 πR3 - 2/3 πr3
= 2/3 π(R3 - r3)
= 2/3 × 22/7 × [(1.01)3−(1)3] m3
= 44/21 × (1.030301 - 1) m3
= (44/21 × 0.030301) m3
= 0.06348 m3(approx)
7. Find the volume of a sphere whose surface area is 154 cm2.
Answer
Let r cm be the radius of the sphere
So, surface area = 154cm2
⇒ 4πr2 = 154
⇒ 4 × 22/7 × r2 = 154
⇒ r2 = (154×7)/(4×22) = 12.25
⇒ r = 3.5 cm
Volume = 4/3 πr3
= (4/3 × 22/7 × 3.5 × 3.5 × 3.5) cm3
= 539/3 cm3
8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹498.96. If the cost of white-washing is ₹2.00 per square metre, find the
(i) inside surface area of the dome, (ii) volume of the air inside the dome.
Answer
(i) Inside surface area of the dome =Total cost of white washing/Rate of white washing
= (498.96/2.00) m2 = 249.48 m2
(ii) Let r be the radius of the dome.
Surface area = 2πr2
⇒ 2 × 22/7 × r2 = 249.48
⇒ r2 = (249.48×7)/(2×22) = 39.69
⇒ r2= 39.69
⇒ r = 6.3m
Volume of the air inside the dome = Volume of the dome
= 2/3 πr3
= (2/3 × 22/7 × 6.3 × 6.3 × 6.3) m3
= 523.9 m3 (approx.)
9. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S′. Find the
(i) radius r′ of the new sphere, (ii) ratio of S and S′.
Answer
(i) Volume of 27 solid sphere of radius r = 27 × 4/3 πr3 --- (i)
Volume of the new sphere of radius r′ = 4/3 πr'3 --- (ii)
A/q,
4/3 πr'3= 27 × 4/3 πr3
⇒ r'3 = 27r3
⇒ r'3 = (3r)3
⇒ r′ = 3r
(ii) Required ratio = S/S′ = 4 πr2/4πr′2 = r2/(3r)2
= r2/9r2 = 1/9 = 1:9
10. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Answer
Diameter of the spherical capsule = 3.5 mm
Radius(r) = 3.52mm
= 1.75mm
Medicine needed for its filling = Volume of spherical capsule
= 4/3 πr3
= (4/3 × 22/7 × 1.75 × 1.75 × 1.75) mm3
= 22.46 mm3 (approx.)
7. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Answer
On revolving the ⃤ ABC along the side 12 cm, a right circular cone of height(h) 12 cm, radius(r) 5 cm and slant height(l) 13 cm will be formed.
Volume of solid so obtained = 1/3 πr2h
= (1/3 × π × 5 × 5 × 12) cm3
= 100π cm3
8. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Answer
On revolving the ⃤ ABC along the side 12 cm, a cone of radius(r) 12 cm, height(h) 5 cm, and slant height(l) 13 cm will be formed.
Volume of solid so obtained =1/3 πr2h
= (1/3 × π × 12 × 12 × 5) cm3
= 240π cm3
Ratio of the volumes = 100π/240π = 5/12 = 5:12
9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Answer
Diameter of the base of the cone = 10.5 m
Radius (r) = 10.5/2 m = 5.25 m
Height of the cone = 3 m
Volume of the heap = 1/3 πr2h
= (1/3 × 22/7 × 5.25 × 5.25 × 3) m3
= 86.625 m3
Also,
l2 = h2 + r2
⇒ l2 = 32 + (5.25)2
⇒ l2 = 9 + 27.5625
⇒ l2 = 36.5625
⇒ l = √36.5625 = 6.05 m
Area of canvas = Curve surface area
= πrl = (22/7 × 5.25 × 6.05) m2
= 99.825 m2 (approx)
Page No: 236
Exercise 13.8
1. Find the volume of a sphere whose radius is
(i) 7 cm (ii) 0.63 m
Answer
(i) Radius of the sphere(r) = 7 cm
Therefore, Volume of the sphere = 4/3 πr3
= (4/3 × 22/7 × 7 × 7 × 7) cm3
= 4312/3 cm3
(ii) Radius of the sphere(r) = 0.63 m
Volume of the sphere = 4/3 πr3
= (4/3 × 22/7 × 0.63 × 0.63 × 0.63) m3
= 1.05 m3
2. Find the amount of water displaced by a solid spherical ball of diameter.
(i) 28 cm (ii) 0.21 m
Answer
(i) Diameter of the spherical ball = 28 cm
Radius = 28/2 cm = 14 cm
Amount of water displaced by the spherical ball = Volume
= 4/3 πr3
= (4/3 × 22/7 × 14 × 14 × 14) cm3
= 34496/3 cm3
(ii) Diameter of the spherical ball = 0.21 m
Radius (r) = 0.21/2 m = 0.105 m
Amount of water displaced by the spherical ball = Volume
= 4/3 πr3
= (43×227×0.105×0.105×0.105) m3
= 0.004851 m3
3. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
Answer
Diameter of the ball = 4.2 cm
Radius = (4.2/2) cm = 2.1 cm
Volume of the ball = 4/3 πr3
= (4/3 × 22/7 × 2.1 × 2.1 × 2.1) cm3
= 38.808 cm3
Density of the metal is 8.9g per cm3
Mass of the ball = (38.808 × 8.9) g = 345.3912 g
4. The diameter of the moon is approximately one-fourth of the diameter of the earth.What fraction of the volume of the earth is the volume of the moon?
Answer
Let the diameter of the moon be r
Radius of the moon = r/2
A/q,
Diameter of the earth = 4r
Radius(r) = 4r/2 = 2r
Volume of the moon = v = 4/3 π(r/2)3
= 4/3 πr3 × 1/8
⇒ 8v = 4/3 πr3 --- (i)
Volume of the earth = r3 = 4/3 π(2r)3
= 4/3 πr3× 8
⇒ V/8 = 4/3 πr3 --- (ii)
From (i) and (ii), we have
8v = V/8
⇒ v = 1/64 V
Thus, the volume of the moon is 1/64 of the volume of the earth.
5. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Answer
Diameter of a hemispherical bowl = 10.5 cm
Radius(r) = (10.5/2) cm = 5.25cm
Volume of the bowl = 2/3 πr3
= (2/3 × 22/7 × 5.25 × 5.25 × 5.25) cm3
= 303.1875 cm3
Litres of milk bowl can hold = (303.1875/1000) litres
= 0.3031875 litres (approx.)
6. A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Answer
Internal radius = r = 1m
External radius = R = (1 + 0.1) cm = 1.01 cm
Volume of iron used = External volume – Internal volume
= 2/3 πR3 - 2/3 πr3
= 2/3 π(R3 - r3)
= 2/3 × 22/7 × [(1.01)3−(1)3] m3
= 44/21 × (1.030301 - 1) m3
= (44/21 × 0.030301) m3
= 0.06348 m3(approx)
7. Find the volume of a sphere whose surface area is 154 cm2.
Answer
Let r cm be the radius of the sphere
So, surface area = 154cm2
⇒ 4πr2 = 154
⇒ 4 × 22/7 × r2 = 154
⇒ r2 = (154×7)/(4×22) = 12.25
⇒ r = 3.5 cm
Volume = 4/3 πr3
= (4/3 × 22/7 × 3.5 × 3.5 × 3.5) cm3
= 539/3 cm3
8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹498.96. If the cost of white-washing is ₹2.00 per square metre, find the
(i) inside surface area of the dome, (ii) volume of the air inside the dome.
Answer
(i) Inside surface area of the dome =Total cost of white washing/Rate of white washing
= (498.96/2.00) m2 = 249.48 m2
(ii) Let r be the radius of the dome.
Surface area = 2πr2
⇒ 2 × 22/7 × r2 = 249.48
⇒ r2 = (249.48×7)/(2×22) = 39.69
⇒ r2= 39.69
⇒ r = 6.3m
Volume of the air inside the dome = Volume of the dome
= 2/3 πr3
= (2/3 × 22/7 × 6.3 × 6.3 × 6.3) m3
= 523.9 m3 (approx.)
9. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S′. Find the
(i) radius r′ of the new sphere, (ii) ratio of S and S′.
Answer
(i) Volume of 27 solid sphere of radius r = 27 × 4/3 πr3 --- (i)
Volume of the new sphere of radius r′ = 4/3 πr'3 --- (ii)
A/q,
4/3 πr'3= 27 × 4/3 πr3
⇒ r'3 = 27r3
⇒ r'3 = (3r)3
⇒ r′ = 3r
(ii) Required ratio = S/S′ = 4 πr2/4πr′2 = r2/(3r)2
= r2/9r2 = 1/9 = 1:9
10. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Answer
Diameter of the spherical capsule = 3.5 mm
Radius(r) = 3.52mm
= 1.75mm
Medicine needed for its filling = Volume of spherical capsule
= 4/3 πr3
= (4/3 × 22/7 × 1.75 × 1.75 × 1.75) mm3
= 22.46 mm3 (approx.)

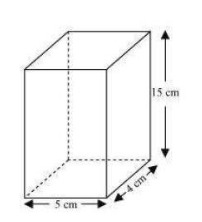 Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) Of tin can = 15 cm
Capacity of tin can l x b x h
(5 x 4 x 15)
Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) Of tin can = 15 cm
Capacity of tin can l x b x h
(5 x 4 x 15) 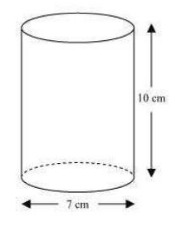 Radius (r) of circular end of plastic cylinder
Radius (r) of circular end of plastic cylinder 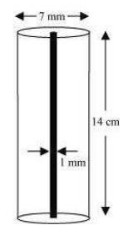 Radius (r) of pencil =
Radius (r) of pencil =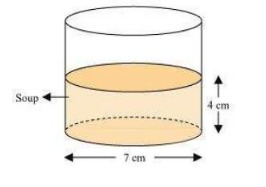 Radius (r) of cylindrical bowl =
Radius (r) of cylindrical bowl =